Значение кривизны пространства
Математик Вильям Клиффорд (1845-1879) переводил труды Римана на английский язык и в процессе этой работы был очарован идеями Римана о связи между физическими явлениями и геометрией. Он стал развивать эти идеи. Читая лекцию в Кембриджском философском обществе, посвященную «науке о пространстве», он обсуждал нашу возможность судить о геометрии пространства на астрономических масштабах и на масштабах столь малых, что они недоступны для наблюдения (то есть в мире элементарных частиц).
>
При этом он утверждал, что «малые области пространства фактически похожи на небольшие холмики на поверхности, которая в среднем плоская, таким образом, обычные законы геометрии к ним неприменимы». Он полагал, что «это свойство искривленности или искаженности непрерывно передается от одной области пространства к другой наподобие волны» и что «изменение кривизны пространства — это как раз то, что реально происходит в явлении, которое мы называем движением материи».
Клиффорд заключил, что весь физический мир (движение всей материи) есть результат этого свойства пространства. Для того времени его идеи были революционными, поскольку само понятие пространство еще не было осознано многими учеными. В год рождения Эйнштейна умер Клиффорд. Он был совсем молод и не сумел более глубоко разработать свою идею. Его видение мира опередило общую теорию относительности на 40 лет.
Отправной точкой для общей теории относительности Эйнштейна стал закон Галилея о том, что все тела падают с одинаковым ускорением независимо от их массы (если пренебречь трением о воздух). Это эмпирическое правило можно понять как следствие Второго закона Ньютона (сила равна массе, умноженной на ускорение) и Ньютонова закона гравитации (сила тяготения пропорциональна массе тела). Оба эти закона содержат один и тот же коэффициент пропорциональности — массу тела, поэтому ускорение падающего вниз тела не зависит от его массы. Но раз мы имеем дело с двумя независимыми законами природы, то должны поинтересоваться: как получилось, что оба они содержат один и тот же коэффициент.
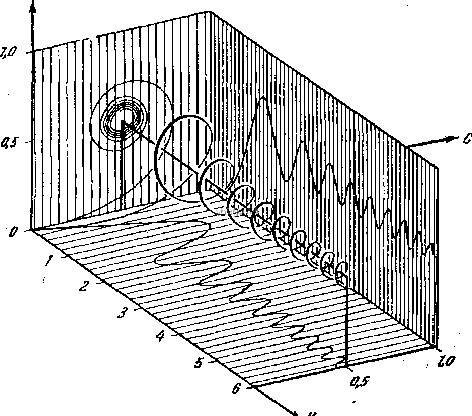
Согласно Эйнштейну, это неслучайно. Закон Галилея имеет глубокий смысл, он показывает, что гравитация не реальная сила, а лишь фиктивная. Нам уже знакомы фиктивные силы: например,
Кориолисова сила, описанная французским физиком Гаспаром Кориолисом (17921843). В Северном полушарии ветры, дующие с юга, пытаются повернуть на восток, а дующие с севера поворачивают на запад. Это приводит к вращению воздушных потоков против часовой стрелки вокруг областей низкого давления. Сила Кориолиса — это всего лишь проявление вращения Земли вокруг оси, а вовсе не реальная сила. Для фиктивных сил свойственно, что они сообщают одинаковое ускорение всем телам независимо от их характеристик, таких как масса, электрический заряд и т. п.
Точно так же ускорение силы тяжести не зависит от свойств тела. Фиктивную силу легко исключить (в принципе); например, если остановить вращение Земли, то сила Кориолиса пропадет. А гравитация исчезает при свободном падении. В свободно падающей кабине мы не чувствуем свой вес, например — в кабине лифта, когда рвется его трос, а тормоза отказывают. Вдали от Земли можно искусственно создать такую же силу тяжести, как на земной поверхности, если заставить космический корабль двигаться с ускорением 9,8 м/с2, равным тому ускорению земной гравитации, которое мы обычно испытываем.
Эйнштейн пришел к выводу, что если ускорение силы тяжести так легко создать и уничтожить, то оно должно быть отражением какогото более глубокого явления. Этим явлением, по мнению Эйнштейна, является кривизна пространства. Материя заставляет окружающее пространство искривляться, а тела реагируют на эту кривизну таким образом, что это выглядит как действие гравитации.
 Свойства неевклидовых геометрий
Свойства неевклидовых геометрий Открытие неевклидовых геометрий
Открытие неевклидовых геометрий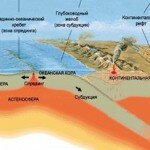 Гравитационные волны
Гравитационные волны Странные свойства черных дыр
Странные свойства черных дыр



Добавить комментарий