Свойства неевклидовых геометрий

Вселенная конечна или бесконечна? Это не такто просто «уви­деть». Евклидова геометрия прекрасно описывает наши обычные измерения. Но в будничной геометрии трудно встретиться с бес­конечностью. С другой стороны, испытываешь немалые трудности, пытаясь представить себе конечный мир со сферической геометри­ей, хотя его конечность легко описывается математически.

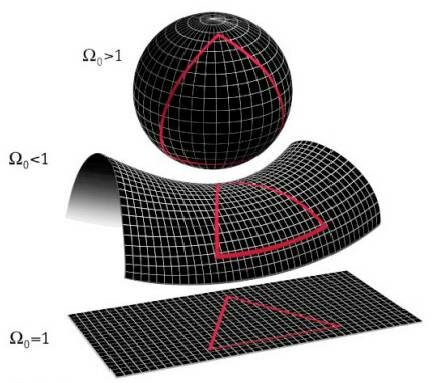
Обычно для демонстрации неевклидовой геометрии в качестве примера используют поверхности. Наша трехмерная Вселенная (мы не учитываем время) в практическом отношении плоская, поэтому в ней мы легко можем заметить кривизну обычных поверхностей. Но трудно представить четырехмерное пространство, не разбираясь в том, что означает кривизна. Наш мозг не привык решать такие задачи, поэтому лучше ограничиться рассмотрением двумерных поверхностей. Сферическая Вселенная имеет странное свойство — у нее конечный объем, хотя ни в каком направлении невозможно найти ее край. Это легче понять, если представить поверхность сфе­ры, которая позволяет нам заметить и другое интересное свойство сферической геометрии: идущий вперед путешественник вернется в начальную точку своего пути после того, как обойдет вокруг света. Путешествуя по Земле, если вы движетесь все время вперед по боль­шому кругу, вы тоже вернетесь в исходную точку. Странный резуль­тат, если вы считаете Землю плоской!

Как легко понять, двумерным аналогом сферической Вселен­ной служит поверхность сферы. Не обязательно иметь возможность взглянуть на нее из третьего измерения или же обходить сферу кру­гом, чтобы догадаться о кривизне сферической поверхности. Суще­ство, живущее на сферической поверхности, не способное выйти в третье измерение над этой поверхностью и даже не имеющее пред­ставления об этом третьем измерении, все равно может проводить построения на этой поверхности, чтобы узнать ее геометрические свойства. Оно может нарисовать треугольник и измерить сумму его внутренних углов. Если результат получится больше 1800, это дока­жет, что существо живет на сферической поверхности (рис 15.3) Или так: можно нарисовать круг и измерить его. Если отношение длины окружности к ее диаметру меньше, чем л (= 3,141592…), то существо будет знать, что оно живет в мире сферической геометрии.

В противном случае, если сумма внутренних углов треугольника меньше чем 1800, а отношение длины окружности к ее диаметру боль­ше л и если через данную точку можно провести любое число линий, параллельных данной линии, то существо понимает, что оно живет в гиперболическом пространстве. Гиперболическое пространство тя­нется на бесконечное расстояние и не имеет аналога в обычной жиз­ни. Форма седла, точнее — его центральной части, более или менее напоминает ограниченную область гиперболической поверхности.

Границей между сферическими и гиперболическими поверхно­стями служит плоская поверхность, или двумерное евклидово про­странство. Привычные для нас законы евклидовой геометрии спра­ведливы в этом и только в этом пространстве: сумма внутренних углов треугольника точно равна 1800, отношение длины окружности к ее радиусу в точности равно л, а через точку можно провести одну и только одну прямую, параллельную другой прямой (