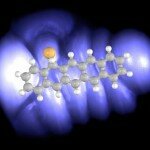
Расплывчатые частицы: принцип неопределенности Гейзенберга
Главная особенность квантовой механики заключена в ее вероятностной природе, сформулированной Максом Борном в 1926 году. Вместо того чтобы говорить о точных значениях физических величин, есть возможность описать только распределение вероятности этих значений. Связано это с Принципом неопределенности, Опубликованным Гейзенбергом в 1927 году.
Механика атомов
Новая теория для механики атомных явлений была названа квантовой механикой. Первый шаг к ее открытию сделал немецкий физик Вернер Гейзенберг. Немного позже была разработана квантовая электродинамика для описания электромагнитных явлений в мире атомов. Эти новые теории связаны со старой, так называемой классической физикой таким образом, что если двигаться от масштаба атомов к обычным размерам, то в пределе получаются результаты классической физики. Читать далее
Модель Бора и спектроскопические законы Кирхгофа
Модель атома Бора прекрасно объясняет экспериментальные законы спектроскопии, открытые Кирхгофом. В тонком слое горячего газа атомы сталкиваются друг с другом, забрасывая электроны на высокие орбиты. Вскоре они спрыгивают на орбиты нижних уровней. В результате атом излучает’ фотоны, энергия которых соответствует разности энергий орбит.
Атом Бора
Датский физик Нильс Бор применил новую квантовую концепцию к атому. Бор родился в Копенгагене, в богатой семье. В юности он был известным футболистом: вместе с братом играл в лучших национальных командах. Бор учился в Копенгагенском университете и защитил диссертацию в 1911 году. Поворотной точкой в его карьере стала работа в Англии после защиты диссертации. Вначале Бор поехал в Кембридж, но после знакомства с Резерфордом решил переехать в Манчестер. Читать далее
Единство волн и частиц
Проникнув в тайны строения вещества, мы вновь можем вернуться к свету. Как нам уже известно, в XIX веке волновая теория восторжествовала над более ранней теорией Ньютона о частицах света — корпускулах. Но для волны нужна среда, в которой может распространяться волна. Для звуковых волн нужен воздух, а в космосе нет ни звуковых волн, ни воздуха. Предполагалось, что средой для световых волн служит эфир, заполняющий космос, но эта идея лишь усложняла проблему. Читать далее
Гравитационные волны
Одним из явлений, связанных с эластичностью пространства, являются гравитационные волны — небольшие изменения кривизны пространства, распространяющиеся со скоростью света. Хотя американский физик Джозеф Вебер (1919-2000) еще в 1967 году утверждал, что открыл гравитационные волны, в действительности до сих пор нет прямого подтверждения их обнаружения.
Странные свойства черных дыр
В нашем мире, как описывает его общая теория относительности, есть много странного; одно из самых удивительных — черная дыра. Если тело сжимается все сильнее и сильнее, то гравитация на его поверхности усиливается. Давайте для примера рассмотрим Землю.
Следствия общей теории относительности
Зная геометрию пространства, можно вычислить орбиту тела, на которое не действует ничто кроме гравитации. Теперь мы не считаем гравитацию силой, а говорим о свободном движении. В плоском пространстве такое движение происходит по прямой линии, но в искривленном пространстве свободное движение может происходить практически по замкнутой орбите. Возьмем обращающуюся вокруг Солнца планету. Она движется вперед по прямой, то есть по кратчайшему пути, но так как Солнце искривило пространство, орбита планеты становится эллипсом.
Значение кривизны пространства
Математик Вильям Клиффорд (1845-1879) переводил труды Римана на английский язык и в процессе этой работы был очарован идеями Римана о связи между физическими явлениями и геометрией. Он стал развивать эти идеи. Читая лекцию в Кембриджском философском обществе, посвященную «науке о пространстве», он обсуждал нашу возможность судить о геометрии пространства на астрономических масштабах и на масштабах столь малых, что они недоступны для наблюдения (то есть в мире элементарных частиц).
Свойства неевклидовых геометрий
Вселенная конечна или бесконечна? Это не такто просто «увидеть». Евклидова геометрия прекрасно описывает наши обычные измерения. Но в будничной геометрии трудно встретиться с бесконечностью. С другой стороны, испытываешь немалые трудности, пытаясь представить себе конечный мир со сферической геометрией, хотя его конечность легко описывается математически.