Момент Земли
Определение момента инерции Земли.
Из-за экваториального вздутия не только форма геоида, но и форма всех гравитационных поверхностей вне Земли слегка отличается от сферической. Поскольку гравитационная сила по определению перпендикулярна эквипотенциальной поверхности, сила притяжения, действующая между Землей и любым телом В в пространстве, таким, как Луна, Солнце или спутник, не направлена точно к центру Земли (если только тело В не лежит в экваториальной плоскости Земли или на ее оси).  Это притяжение F равно сумме большой силы Fc, которая направлена вдоль линии, соединяющей центры тел, и значительно меньшей силы FT, направленной под прямым углом к этой линии. Из ньютоновского третьего закона движения, гласящего, что действие и противодействие равны по величине и противоположны по направлению, следует, что Земля должна испытывать соответствующее воздействие со стороны тела В. Притяжение FRнаправленное к центру Земли, уравновешивается центробежной силой, но малые силы FTне уравновешиваются, и вместе они создают вращающий момент, который стремится двигать тело В по часовой стрелке (рис. 3.5) и поворачивать Землю против часовой стрелки.
Это притяжение F равно сумме большой силы Fc, которая направлена вдоль линии, соединяющей центры тел, и значительно меньшей силы FT, направленной под прямым углом к этой линии. Из ньютоновского третьего закона движения, гласящего, что действие и противодействие равны по величине и противоположны по направлению, следует, что Земля должна испытывать соответствующее воздействие со стороны тела В. Притяжение FRнаправленное к центру Земли, уравновешивается центробежной силой, но малые силы FTне уравновешиваются, и вместе они создают вращающий момент, который стремится двигать тело В по часовой стрелке (рис. 3.5) и поворачивать Землю против часовой стрелки.
Можно дать и другое объяснение этому крутящему моменту земли
Можно дать и другое объяснение этому крутящему моменту, не используя представления об эквипотенциальных поверхностях, а рассматривая одну сильно упрощенную модель.. Притяжение между телом В и каждой из этих масс не совсем одинаково из-за различия в расстоянии. Как показано на рисунке, это небольшое отличие F1 от Fi придает Земле малый крутящий момент против часовой стрелки, а следовательно (в виде реакции), и момент, который будет стремиться двигать тело В вокруг Земли по часовой стрелке. Используя уравнение, мы можем подсчитать эти силы, а значит, и моменты, если, конечно, нам известны все рассматриваемые массы и расстояния. Мы получим те же самые результаты, что и раньше, когда мы рассчитывали эквипотенциальные поверхности вблизи тела В, а затем находили силы, направленные перпендикулярно этим поверхностям.
На практике используется метод потенциалов
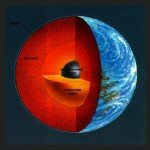
На практике используется метод потенциалов, так как заменить экваториальное вздутие каким-то числом точечных масс непросто. Главное, что надо отметить,-это то, что чем больше момент инерции Земли относительно ее оси вращения, тем больше крутящий момент. Это происходит потому, что чем больше момент инерции, тем, очевидно, большая часть масск Земли оказывается удаленной от ее оси; в свою очередь чем дальше находится масса от оси, тем больше центробежная сила, приложенная к этой массе, и, следовательно, тем крупнее экваториальное вздутие.
Крутящий момент земли зависит также от массы внешнего тела и от расстояния до него
Крутящий момент зависит также от массы внешнего тела и от расстояния до него. В случае искусственного спутника этот момент чрезвычайно мал и поэтому оказывает совсем незначительное влияние на Землю. Однако воздействие Земли на спутник очень заметно, так как оно возмущает его орбиту, что позволяет нам установить, как меняется притяжение Земли в пространстве, и, следовательно, позволяет судить о форме геоида, о чем уже упоминалось в предыдущем разделе. Самый большой вращающий момент в Земле создается Луной, меньшей величины момент-Солнцем, поскольку хотя Солнце и больше, но расположено оно дальше, и расстояние сказывается сильнее, чем масса.
Под действием вращающего момента, создаваемого Луной, земная ось не сохраняет свою ориентировку неизменной
Может показаться очевидным, что крутящее воздействие Луны (или Солнца) на экваториальное вздутие Земли должно двигать оба тела, пока Луна не окажется в экваториальной плоскости Земли, где вращающий момент равен нулю. Действительно, так и было бы, если бы Земля не вращалась, но поскольку она вращается, то ведет себя как волчок-один из тех игрушечных гироскопов, которые раскачиваются во все стороны, как бы не считаясь с силой тяжести. На рис. 3.7 видно, что вес волчка и реакция его опоры образуют вращающий момент, который должен был бы привести к падению волчка на бок, если бы он не вращался. Однако мы знаем, что, вращаясь, волчок раскачивается, или испытывает прецессию, так что его ось описывает коническую поверхность. Подобным же образом, под действием вращающего момента, создаваемого Луной, земная ось не сохраняет свою ориентировку неизменной, а находится в состоянии медленной прецессии, причем ось конуса прецессии перпендикулярна плоскости орбиты Земли.
Если приведенные выше рассуждения сопроводить количественным анализом, можно вывести математическое выражение для скорости прецессии. Оно содержит такие величины, как масса Луны (или другого тела) и расстояние до нее, а также два дополнительных условия. Одно из них показывает, как вращающий момент и, следовательно, скорость прецессии зависят от того, насколько гравитационное поле Земли отклоняется от полной симметрии, а это мы можем установить по движению спутников или из других определений формы геоида. Другое условие показывает, что скорость прецессии обратно пропорциональна моменту инерции Земли относительно оси ее вращения. Таким образом, момент инерции Земли можно вычислить, исходя из измерений скорости прецессии.
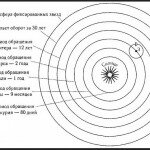
Скорость прецессии Земли мала, потому что относительно мало экваториальное вздутие и велико расстояние до Луны: один полный цикл прецессии занимает около 26 тыс. лет. Прецессию можно земетить, так как хотя земная ось в настоящее время указывает почти точно на Полярную звезду , положение оси все же медленно меняется.
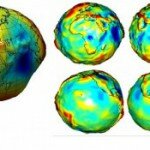 Форма Земли
Форма Земли